Определение прямой в математике является важным элементом и используется для построения фигур, графиков функций и необходимых расчетов для прямо пропорциональных величин. Однако не все учащиеся понимают, какой смысл ее применения в различных дисциплинах. В интернете проблематично найти систематизированную информацию на эту тему. Для качественного обучения нужно рассмотреть основные понятия и аксиомы.
Общие сведения
Точка — это базовая единица геометрии. Она обозначается заглавными литерами латинского алфавита (S, T, A и т. д. ) и предназначена для построения прямых (линий), отрезков, лучей, углов и прочих фигур.
Прямая — геометрическое место точек, при соединении которых образуется линия без искажений, неограниченная в пространстве. Она бесконечна, поскольку не имеет начала и конца, и обозначается прописными буквами (s, t, a, b и т. д. ).
С ее помощью получаются следующие фигуры и элементы:
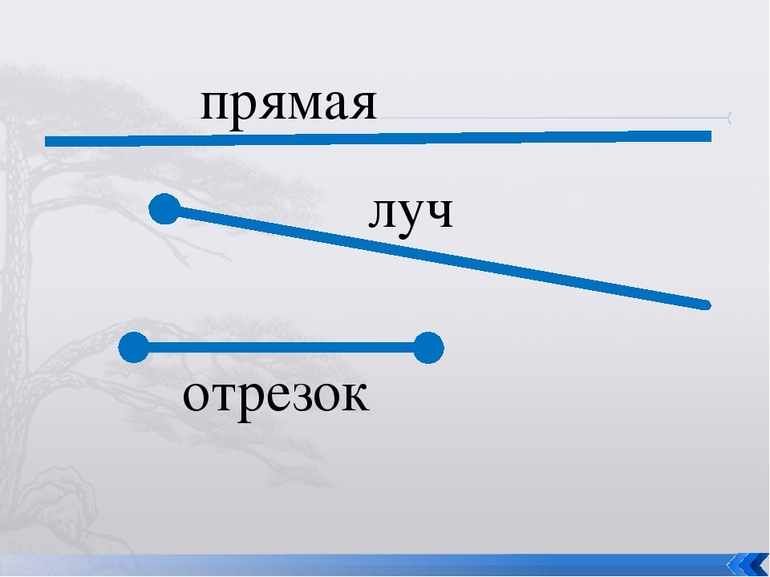
- Лучи.
- Отрезки.
- Треугольники.
- Четырехугольники.
- Многоугольники.
- Плоскости.
- Объемные фигуры: параллелепипед, куб и т. д.
Кроме того, она известна в дисциплинах с физико-математическим уклоном, как линейная зависимость величин. Луч — часть линии, исходящей из одной точки.
Алгоритм построения выглядит следующим образом:
- Отмечается любая точка (M).
- Из нее проводится прямая.
Из геометрического построения можно сделать вывод, что M — левая или правая граница, из которой исходит линия, устремляющаяся в бесконечность. Если на луче отметить еще одну точку, получится отрезок (часть линии или луча, ограниченная с двух сторон). Его обозначение состоит из двух букв (АВ). В этом случае прямую можно обозначить также двумя литерами АВ (АБ). Следует отметить, что она также бывает и ломаной линией.
Прямо пропорциональная зависимость
Существует понятие о прямой пропорциональности двух или нескольких величин. В качестве коэффициента пропорциональности выступает определенное число.
Прямо пропорциональную зависимость еще называют линейной функцией, графиком которой является луч или отрезок. Чтобы написать выражение, характеризующее ее, нужно знать формулу, имеющую следующий вид: s = k * t + m, где s — зависимая переменная, к — коэффициент пропорциональности, t — аргумент (независимый коэффициент) и m — константа (свободный член).
Коэффициент «m» может принимать любые значения. Расположения линии зависит от k и m. В этом случае нужно разобрать некоторые свойства:
- При m=0 график будет проходить через начало декартовой системы координат.
- Если k>,0, значения угла наклона луча относительно оси аргументов находится в пределах от 0 до 90 градусов.
- Когда k<,0 и m эквивалентен некоторому значению (не равен 0), угол наклона, описанный во втором свойстве, будет тупым.
- При равенстве к=0 линия || оси абсцисс (аргументов).
В геометрии величина «к» называется угловым коэффициентом и вычисляется через тангенс угла наклона (f) по формуле: tg (g)=(m/k)+(k-m)/2k.
Таким образом, прямая линия нужна не только для построения различных фигур, но и графиков прямо пропорциональности двух и более физических величин.