Перевод чисел на язык, который понятен любой электронно-вычислительной машине, осуществляется по определенному алгоритму в некоторое представление. Наиболее востребованными являются двоичная, шестнадцатеричная, а также восьмеричная системы счисления. Однако перед переходом к практике специалисты рекомендуют рассмотреть теорию конвертации первой и последней формы информации (2 и 8).

Общие сведения
Для работы с системами счисления (СС) необходимо разобрать их классификацию, а также базовые определения представления числовой информации. В математике существуют 2 понятия: цифра и число. Первое — базовая единица или символ, при комбинации которого можно записать любое значение.

Цифры бывают только двух типов: римскими и арабскими. Однако наибольшее применение получили последние, поскольку используются при выполнении расчетов, записи результатов и т. д. Римские применяются в основном для обозначения величин, на которые требуется обратить внимание. Однако они непрактичны, поскольку не все знают их расшифровку. Кроме того, римские величины невозможно представить в экспоненциальной и степенной форме.
Число — количественная характеристика, показывающая фактическое наличие или отсутствие какого-либо предмета, процесса или явления. Например, микропроцессор состоит из 32 миллиардов транзисторов. В примере числом или значением является 32 млрд.
Каждая величина состоит из разрядной сетки, т. е. единиц, десятков, сотен и т. д. При выполнении различных алгебраических операций важно следить за соответствием разрядов одного значения другому. Например, нельзя складывать сотни и единицы, т. к. это приведет к ошибочным вычислениям.
Классификация числовых представлений
Некоторые пользователи-практики могут считать, что нет смысла рассматривать классификацию систем исчисления, но это не так. Новички, начинающие знакомство с представлением числовой информации, должны понимать, что порядок (расположение) разрядов в двоичной и восьмеричной имеет значение. Всего бывает 2 вида СС, к которым относятся позиционные и непозиционные.
Первые зависят от расположения математических символов, которые их составляют. Это утверждение довольно просто доказать. Достаточно взять двузначное число (23), а затем образовать из него второе посредством перестановки десятков и единиц, т. е. 32. После этого произвести обычную математическую операцию их разности: 32-23=9. Из расчетов видно, что 2 значения отличаются между собой. Следовательно, расположение цифр имеет значение для позиционной формы представления информации.

Непозиционная — СС, в которой расположение знаков не влияет на результат. Для примера можно вспомнить известный фильм «Робинзон Крузо», где главный герой вел счет дней, прожитых на необитаемом острове, при помощи обыкновенных «палочек», которые рисовал на стене. После этого он подсчитывал их общее количество. Следует отметить, что их расположение не влияло на результат.
Другим примером непозиционной СС является обучение детей в начальных классах устному счету. Для этой цели применяются палочки, на которых ребенок выполняет операции сложения, вычитания, умножения и даже деления. Следует отметить, что у этой формы представления есть недостатки, которые мешают ей вытеснить позиционную. К ним относятся следующие:
- Невозможность выполнения операций с дробями.
- Работа с небольшими числами.
- Затруднительное выполнение деления и умножения.
Деление в столбик
Наиболее распространенный и простой способ перевода в двоичный код значения из десятичной системы счисления — деление в столбик. Последний имеет такой вид:
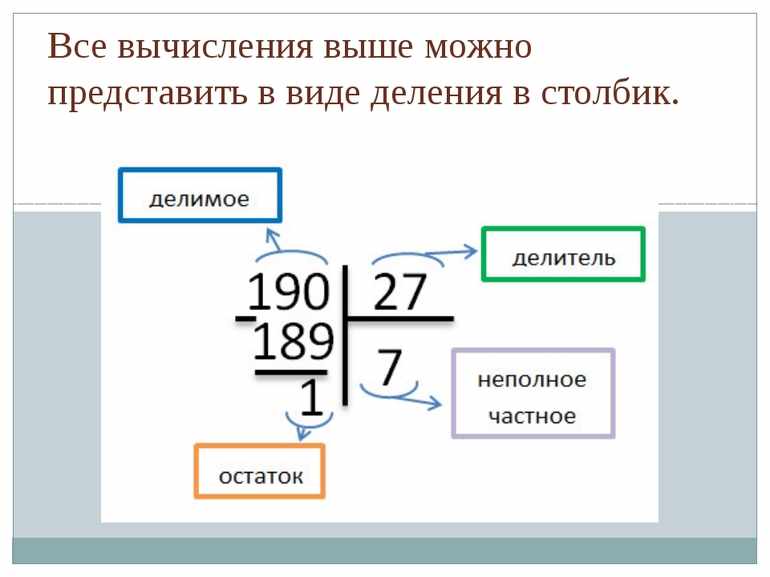
- Записать число в десятичной форме.
- Делить его на 2, записывая нули и единицы: 0 делится, а 1 образуется остаток.
- Написать результат (первый разряд эквивалентен последнему элементу).
Реализацию алгоритма конвертации необходимо разобрать на практическом примере. Например, требуется перевести 123 в двоичную форму. Для этого необходимо следовать определенной методике:
- 123{10}, где {10} система счисления.
- Делить на 2: 123/2 (1).
- 61/2 (1).
- 30/2 (0).
- 15/2 (1).
- 7/2 (1).
- 3/2 (1)
- Остаток: (1).
- Результат записать с остатка, а затем последовательно вверх: 1111011{2}.
Для выполнения обратной операции следует воспользоваться степенным представлением числа, которое начинается справа налево. Если указана единица, то 2 в заданной степени есть. В противном случае — указывается ноль. Реализация методики выглядит следующим образом: 2^0+2^1+0^2+2^3+2^4+2^6=123{10}.
Степенной метод
Второй способ — степенная система. Суть ее заключается в нахождении максимального значения, представленного в целой степени двойки. Для реализации методики необходимо воспользоваться следующим алгоритмом:
- Написать искомое число.
- Найти максимальную степень.
- Отнять от значения в первом пункте величину на втором шаге.
- Повторить 2 и 3, пока не образуется нулевая степень или остаток не будет соответствовать минимуму.
Например, необходимо переводить при помощи степенного способа число 123 в двоичный код. Операция выполняется таким образом:

- 123.
- MAX (1): 2^6=64, поскольку 2^7=128 (больше заданного числа).
- Разность: 123-64=59.
- МАХ (1): 2^5=32.
- 59-32=27.
- МАХ (1): 2^4=16.
- 27-16=11.
- МАХ (1): 2^3=8.
- 11-8=3.
- 2^2 не существует, поскольку 3<,2^2.
- МАХ (1): 2^1=2.
- 3-2=1 (1).
- Искомый результат: 1111011.
Специалисты рекомендуют ознакомиться с каждым из способов преобразования десятичной формы представления в двоичный код. Каждый решает, какой из них больше всего подходит.
Восьмеричная форма
В отличие от шестнадцатеричной формы представления чисел восьмеричная не содержит букв из английского алфавита. В ее основании присутствует 8. Форма получила широкое применение в кодировании текстовой информации. Кодируются и таблицы в восьмеричную систему счисления, различные цветовые оттенки и прочие данные, обладающие небольшими размерами.
Для преобразования из десятичной нужно перевести величину в двоичный код. Далее следовать по такому алгоритму:

- Выделить триады (распределить по 3 разряда).
- Перекодировать группы, записав их в десятичной форме. Когда не хватает количества разрядов, нужно пополнить его нулями.
Для реализации методики нужно рассмотреть пример конвертации 123. Решение задачи имеет такой вид:
- 123.
- {2}: 1111011.
- Группы: {001}{111}{011}.
- {8}: 173.
Операция конвертации выполняется аналогично, но в обратном порядке. Например, необходимо преобразовать 173{8}>,{10}. Решение имеет следующий вид:

- 173{8}.
- Разделяется на элементы: {1}{7}{3}.
- Каждая триада декодируется в исходный двоичный код: {001}{111}{011}.
- Убираются символы группировки и лишние нули: 1111011{2}.
Специалисты в области информационных технологий рекомендуют проверять все решение на веб-сервисах или калькуляторах, работающих с двоичным, восьмеричным и шестнадцатеричным кодами. Их еще называют инженерными. Программы является компонентом всех операционных систем (Linux, Windows и MacOS). При необходимости в интернете можно найти и более удобные версии программного обеспечения для работы с машинными кодами.
Таким образом, восьмеричную СС применяют для кодирования небольших массивов информации. Для конвертации необходимо выполнить промежуточную операцию преобразования десятичной в двоичную форму, а затем разложить последнюю на триады.