 Знания о том, как измерить Землю, появились еще в древности и постепенно оформились в науку геометрию. С греческого языка это слово так и переводится — «землемерие».
Знания о том, как измерить Землю, появились еще в древности и постепенно оформились в науку геометрию. С греческого языка это слово так и переводится — «землемерие».
Мерой протяжённости плоского участка Земли по длине и ширине является площадь. В математике она обычно обозначается латинской буквой S (от англ. «square» — «площадь», «квадрат») или греческой буквой σ (сигма). S обозначает площадь фигуры на плоскости или площадь поверхности тела, а σ площадь поперечного сечения провода в физике. Это основные символы, хотя могут быть и другие, например, в сфере сопротивления материалов, А — площадь сечения профиля.
…
Формулы расчета
 Зная площади простых фигур, можно находить параметры более сложных. Античными математиками были выведены формулы, по которым можно легко их вычислять. Такими фигурами являются треугольник, четырёхугольник, многоугольник, круг.
Зная площади простых фигур, можно находить параметры более сложных. Античными математиками были выведены формулы, по которым можно легко их вычислять. Такими фигурами являются треугольник, четырёхугольник, многоугольник, круг.
Чтобы найти площадь сложной плоской фигуры, её разбивают на множество простых фигур, таких как треугольники, трапеции или прямоугольники. Затем математическими методами выводят формулу для площади этой фигуры. Подобный метод используют не только в геометрии, но и в математическом анализе для вычисления площадей фигур, ограниченных кривыми.
Треугольник
 Начнём с самой простой фигуры — треугольника. Они бывают прямоугольные, равнобедренные и равносторонние. Возьмём любой треугольник ABC со сторонами AB=a, BC=b и AC=c (∆ ABC). Чтобы найти его площадь, вспомним известные из школьного курса математики теоремы синусов и косинусов. Отпуская все выкладки, придём к следующим формулам:
Начнём с самой простой фигуры — треугольника. Они бывают прямоугольные, равнобедренные и равносторонние. Возьмём любой треугольник ABC со сторонами AB=a, BC=b и AC=c (∆ ABC). Чтобы найти его площадь, вспомним известные из школьного курса математики теоремы синусов и косинусов. Отпуская все выкладки, придём к следующим формулам:
- S=√[p•(p-a)•(p-b)•(p-c)] — известная всем формула Герона, где p=(a+b+c)/2 — полупериметр треугольника,
- S=a•h/2, где h — высота, опущенная на сторону a,
- S=a•b•(sin γ)/2, где γ — угол между сторонами a и b,
- S=a•b/2, если ∆ ABC — прямоугольный (здесь a и b — катеты),
- S=b²•(sin (2•β))/2, если ∆ ABC — равнобедренный (здесь b — одно из «бёдер», β — угол между «бёдрами» треугольника),
- S=a²•√¾, если ∆ ABC — равносторонний (здесь a — сторона треугольника).
Четырёхугольник
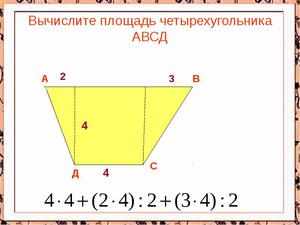
 Пусть имеется четырёхугольник ABCD, у которого AB=a, BC=b, CD=c, AD=d. Чтобы найти площадь S произвольного 4-угольника, нужно разделить его диагональю на два треугольника, площади которых S1 и S2 в общем случае не равны.
Пусть имеется четырёхугольник ABCD, у которого AB=a, BC=b, CD=c, AD=d. Чтобы найти площадь S произвольного 4-угольника, нужно разделить его диагональю на два треугольника, площади которых S1 и S2 в общем случае не равны.
Затем по формулам вычислить их и сложить, т. е. S=S1+S2. Однако, если 4-угольник принадлежит к определённому классу, то его площадь можно найти по заранее известным формулам:
- S=(a+c)•h/2=e•h, если 4-угольник — трапеция (здесь a и c — основания, e — средняя линия трапеции, h — высота, опущенная на одно из оснований трапеции,
- S=a•h=a•b•sin φ=d1•d2•(sin φ)/2, если ABCD — параллелограмм (здесь φ — угол между сторонами a и b, h — высота, опущенная на сторону a, d1 и d2 — диагонали),
- S=a•b=d²/2, если ABCD — прямоугольник (d — диагональ),
- S=a²•sin φ=P²•(sin φ)/16=d1•d2/2, если ABCD — ромб (a — сторона ромба, φ — один из его углов, P — периметр),
- S=a²=P²/16=d²/2, если ABCD — квадрат.
Многоугольник
 Чтобы найти площадь n-угольника, математики разбивают его на простейшие равные фигуры —треугольники, находят площадь каждого из них и затем складывают. Но если многоугольник относится к классу правильных, то используют формулу:
Чтобы найти площадь n-угольника, математики разбивают его на простейшие равные фигуры —треугольники, находят площадь каждого из них и затем складывают. Но если многоугольник относится к классу правильных, то используют формулу:
S=a•n•h/2=a²•n/[4•tg (180°/n)]=P²/[4•n•tg (180°/n)], где n — количество вершин (или сторон) многоугольника, a — сторона n-угольника, P — его периметр, h — апофема, т. е. отрезок, проведённый из центра многоугольника к одной из его сторон под углом 90°.
Круг
Круг — это совершенный многоугольник, имеющий бесконечное число сторон. Нам необходимо вычислить предел выражения справа в формуле площади многоугольника при числе сторон n, стремящемуся к бесконечности. В этом случае периметр многоугольника превратится в длину окружности радиуса R, которая будет границей нашего круга, и станет равен P=2•π•R. Подставим это выражение в указанную выше формулу. Мы получим:
S=(π²•R²•cos (180°/n))/(n•sin (180°/n)).
Найдём предел этого выражения при n→∞. Чтобы это сделать, учтём, что lim (cos (180°/n)) при n→∞ равен cos 0°=1 (lim — знак предела), а lim [1/(n•sin (180°/n))]= lim [1/(n•sin (π/n))] при n→∞ равен 1/π (мы перевели градусную меру в радианную, используя соотношение π рад=180°, и применили первый замечательный предел lim (sin x)/x=1 при x→∞). Подставив в последнее выражение для S полученные значения, придём к известной формуле:
S=π²•R²•1•(1/π)=π•R².
Единицы измерения
 Применяются системные и внесистемные единицы измерения. Системные единицы относятся к СИ (Система Интернациональная). Это квадратный метр (кв. метр, м²) и единицы, производные от него: мм², см², км².
Применяются системные и внесистемные единицы измерения. Системные единицы относятся к СИ (Система Интернациональная). Это квадратный метр (кв. метр, м²) и единицы, производные от него: мм², см², км².
В квадратных миллиметрах (мм²), например, измеряют площадь сечения проводов в электротехнике, в квадратных сантиметрах (см²) — сечения балки в строительной механике, в квадратных метрах (м²) — квартиры или дома, в квадратных километрах (км²) — территории в географии.
Однако иногда используются и внесистемные единицы измерения, такие, как: сотка, ар (а), гектар (га) и акр (ас). Приведём следующие соотношения:
- 1 сотка=1 а=100 м²=0,01 га,
- 1 га=100 а=100 соток=10000 м²=0,01 км²=2,471 ас,
- 1 ас= 4046.856 м²=40,47 а=40,47 соток=0,405 га.