Операция приведения дробей к общему знаменателю в 5 классе используется при выполнении сложения и вычитания, а также для упрощения выражений. Делать это позволяет определенная методика, которой следует придерживаться. Она также оптимизирует вычислительный процесс, экономя драгоценное время и уменьшая число ошибок на начальной стадии обучения. Перед ее изучением математики рекомендуют получить базовые знания.
Базовая информация
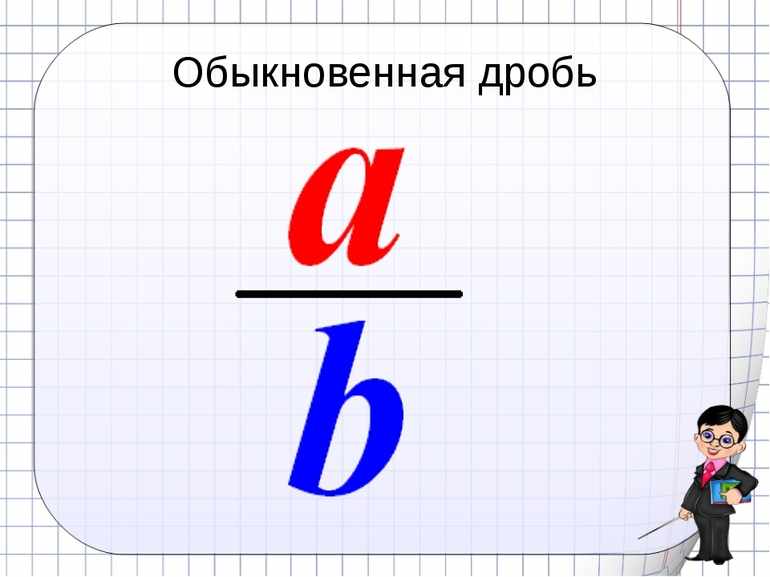
Обыкновенная дробь — значение, состоящее из верхней части (числителя) и нижней (знаменателя). Они разделены чертой. Обыкновенные дробные величины бывают трех типов: правильными, неправильными и смешанными. К первой группе относятся значения, числитель которых меньше знаменателя, ко второй — наоборот. Промежуточным значением является смешанное число. Оно состоит из целой и дробной частей.
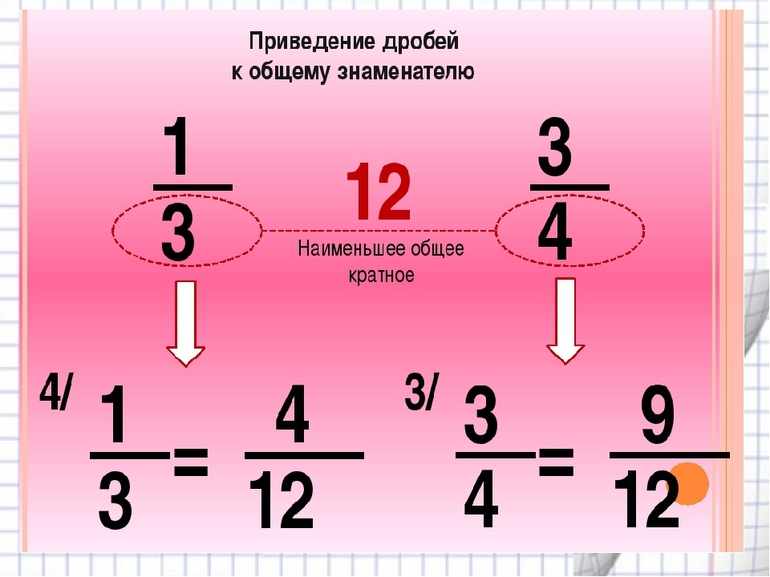
Чтобы выполнить арифметические операции сложения и вычитания, нужно привести дроби к общему знаменателю (ОЗ). Последнее математическое действие обусловлено нахождением наименьшего общего кратного (НОК). Для этой операции могут потребоваться:
- Знание признаков делимости одного числа на другое.
- Умение переводить смешанную дробь в неправильную.
- Разложение на множители.
- Правильно находить коэффициенты для числителей.
Изучение приведения дробей к ОЗ всегда начинается с признаков делимости.
Признаки делимости
Перед ознакомлением с признаками деления чисел нужно внести определенные термины, чтобы учащиеся не путались в правилах. Цифры — математические символы, которые используются для создания чисел. Числа — количественные характеристики, необходимые для выражения фактических данных. У каждого значения существует разрядная сетка (РС). Она состоит из разрядов, именуемых единицами, десятками, сотнями, тысячами и т. д.
Работа со смешанными числами
Для преобразования неправильной дроби в смешанное число используется определенный алгоритм. Он имеет такой вид:

- Поделить числитель на знаменатель, выделив целую часть.
- Перемножить знаменатель и целое значение.
- Отнять от искомого числителя величину, полученную во втором пункте.
Специалисты рекомендуют после алгоритма разобрать его реализацию на примере дробного выражения 25/3. Правильная методика преобразования выглядит следующим образом:
- 25/3=8.
- 3*8=24.
- 8[(25−24)/3]=8[1/3].
Однако нужно уметь выполнять обратную операцию (проверочную) преобразования смешанного числа в неправильную дробь. Для этого требуется выполнить пункты алгоритма в обратном порядке:
- 8[1/3].
- (3*8+1)/3=25/3.
Иными словами, следует умножить знаменатель на целую часть, а затем к результату прибавить числитель.
Приведение к одному знаменателю
Приведение к общему знаменателю — довольно простая операция. Для этого необходимо разобрать все случаи, а также алгоритмы, используемые для этого:
- Одна величина делится на другую без остатка (делимое и делитель).
- Знаменатели — простые числа.
- Состоят из общих множителей.
Общие сомножители
Иногда следует применить все знания, чтобы привести дроби к знаменателю в 8 классе (дисциплина — «алгебра и начало анализа»), который должен быть общим. Выход из ситуации — нахождение НОК. Операция осуществляется по алгоритму:

- Разложение знаменателей на простые элементы.
- Общий знаменатель эквивалентен произведению наименьшего элемента на недостающие сомножители.
- Поиск коэффициентов для числителей и их перемножение.
- Запись искомого результата.
Специалисты рекомендуют разбирать реализацию алгоритма на примере. Для этого следует привести 2 дроби 3/8 и 5/12 к общему знаменателю:
- 8=2*2*2.
- 12=2*2*3.
- НОК=8*3=24.
- Коэффициент для I дробного значения: 3*3/24=9/24.
- Величина, на которую требуется умножить числитель второй дроби: 5*2/24=10/24.
- Результат: 9/24 и 10/24.
Для проверки результатов можно воспользоваться специальными онлайн-сервисами. Однако их математики рекомендуют применять только для сопоставления с ответами, полученными при решении ручным методом без использования средств вычислительной техники.
Таким образом, для приведения дробей к ОЗ необходимо знать признаки делимости, а также основные методики выполнения этой операции.